이재문

1. 선형 시스템

• 선형 시스템: Ax + b와 같은 연립 1차 방정식의 대수적 표현
• Ax + b로의 표현으로는 A, b(linear question)과 x(미지수) 로 표현된다
• 표현은 다음과 같다
  
  1. 선형시스템의 unknown을 모아 열벡터로 표현한다
  2. 선형시스템의 linear equestion에 대해 다음을 수행한다
     • 계수를 모아 A의 행벡터로 표현한다
     • 상수를 모아 b에 의해 표현한다

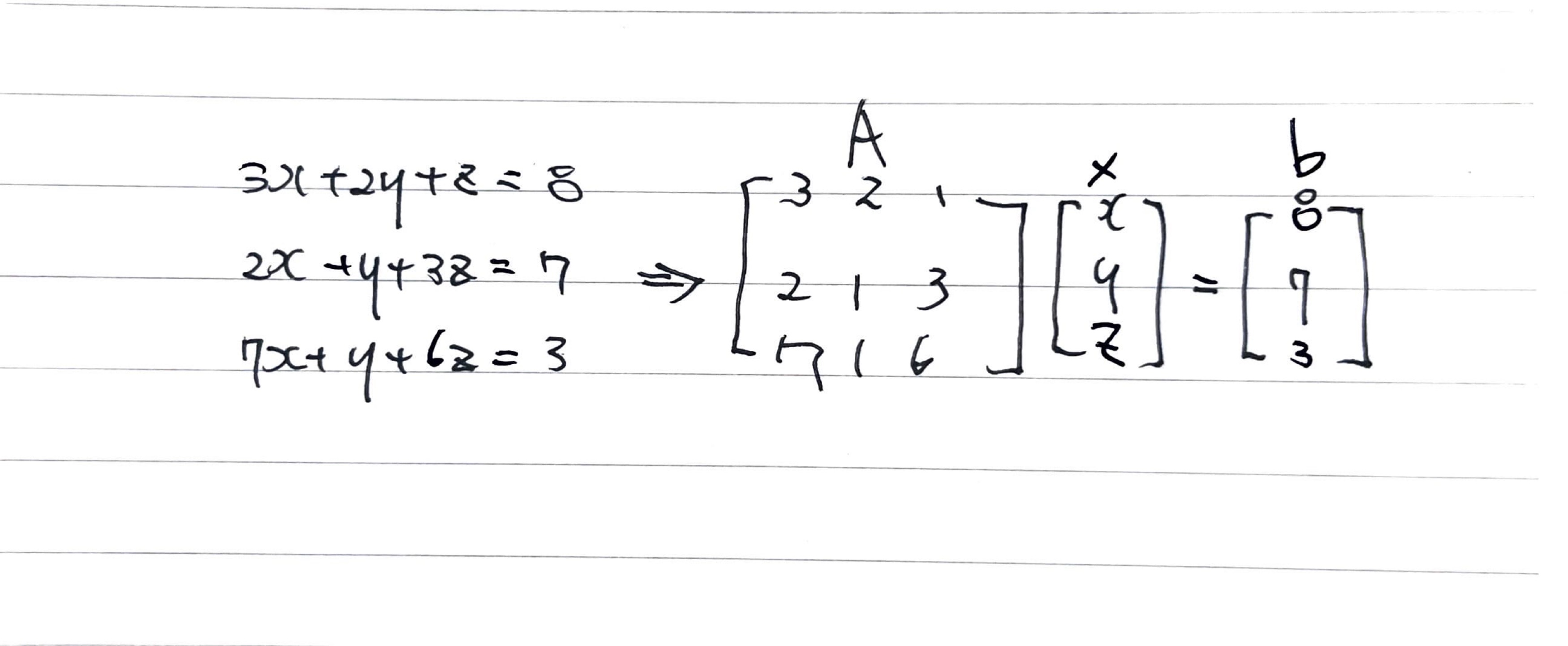
• Ax + b에서 A의 행벡터의 모든 값이 0인 경우 해가 무수히 많거나 해가 없을 수 있다

2. 선형 시스템에서의 해

• 선형 시스템 Ax + b에서의 해는 기본적으로 inverse(A)*b로 구할 수 있다
• 이를 numpy에서 구현하면 아래와 같이 나온다

#numpy 호출
import numpy as np

#행렬 코딩

A = np.array([[3, 1, 1], [1, -2, -1], [1, 1, 1]])
print(A)
print(np.shape(A)) #np.shape = ? x ? 행렬인지 표현

#벡터 코딩
#벡터는 열로 표현하지만 너무 번거롭기 때문에 행으로 표현
b = np.array([4, 1, 2])
print(b)

#역행렬 구하기
# x = A_inv * b
A_inv = np.linalg.inv(A)
print(A_inv)

#역 행렬을 이용한 선형시스템 Ax = b의 해 구하기
x = A_inv @ b

print(x)

#결과 검증
#bb = np.matmul(A, x)
bb = A @ x

print(bb)
print('OK' if np.linalg.norm(b-bb) < 1e-3 else 'Not OK')

3. 가우스 소거법

• 가우스 소거법을 알기전에 필요한 용어로는 아래와 같이 있다
  • 피벗(Pivot, Leading Entry)은 각 행에서 처음으로 나오는 00이 아닌 성분
  • 행사다리꼴(Row Echelon Form Matrix)은 모든 피벗이 다른 열에 위치하고, 모든 성분이 0인 행이 그렇지 않은 행의 앞쪽에 나오는 경우가 존재하지 않으며, 임의의 두 피벗을 비교했을 때 항상 앞쪽 행의 피벗이 앞쪽 열에 위치하는 행렬이다.
  • 기약행사다리꼴(Reduced Row Echelon Form, RREF)은 피벗의 값이 모두 1이고, 피벗과 같은 열에 위치하는 성분은 모두 0인 행사다리꼴이다.
  • 대각행렬(Diagonal Matrix)은 주대각선 이외의 성분이 모두 0인 정사각행렬이다.
    • 출처 : https://00ad-8e71-00ff-055d.tistory.com/61
• 가우스 소거법의 방법으로는 아래와 같이 있다
  • 전방소거법: 주어진 선형시스템을 아래로 갈수록 더 단순한 형태의 선형방정식을 가지도록 변형
  • 후방대입법: 아래에서부터 위로 미지수의 실제값을 대치한다

• 전방 소거법의 절차로는 아래의 방법을 통해 진행 된다
  1. 각열의 행의 값을 pivot으로 잡기
  2. 스케일링을 통해 pivot과 같은 배수값으로 변경
  3. 치환으로 식을 바꾸기
  4. 4교환을 통해 다음 열의 pivot항의 값이 0이 되지 않게 교환
  5. 제일 밑항까지 반복
• 가우스 소거법의 대표적인 PS문제가 있는데 다음과 같다 https://www.acmicpc.net/problem/22940

• 다음 문제에 대한 해결 방법은 다음과 같다 (후방 대입법은 이분을 참고 하였다 / https://guru.tistory.com/54

import sys
def input():
    return sys.stdin.readline().rstrip()

def gauss(A, x):
    n = len(A)
    for i in range(n):
        # 전방 소거법
        # A[i][i]와 A[j][i] 같게 만든 후 나머지 항들을 빼준다
        for j in range(i+1, n):
            div = A[j][i]/A[i][i]
            for k in range(n+1):
                A[j][k] -= div*A[i][k]

    #후방 대입법
    for i in range(n-1, -1, -1):
        x[i] = A[i][n]
        for j in range(i+1, n):
            x[i] -= A[i][j] *x[j]
        x[i] /= A[i][i]

N = int(input())

A = [list(map(int, input().split())) for i in range(N)]

X = [0 for i in range(N)]

gauss(A,X)

ans = [round(i) for i in X]

print(*ans)

• Rank 시스템: 가우스 소거법의 전방소거법을 통해 의미 있는 식의 갯수를 알려주는 시스템
  • Rank의 수의 따라 판별 할 수 있는 해의 갯수가 달라진다

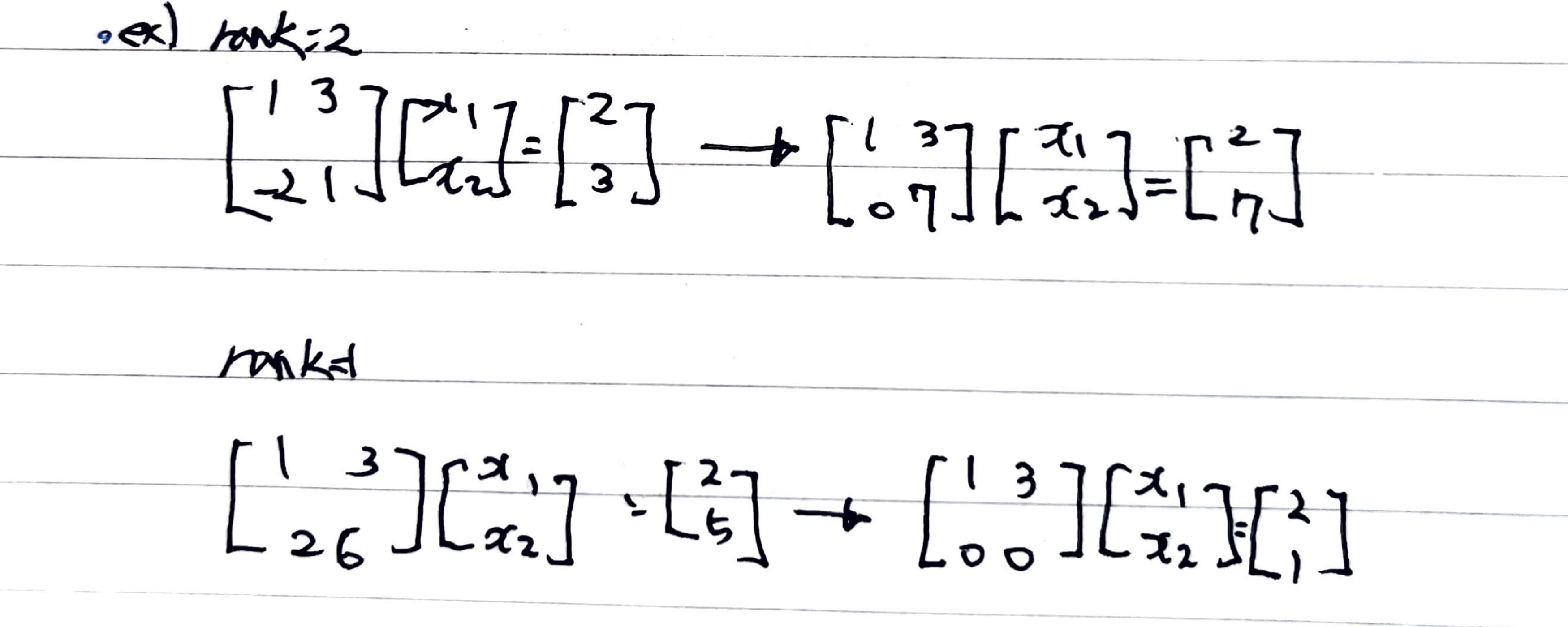
4.  LU분해

• 주어진 행렬을 상삼각행렬과 하 삼각행렬의 곱으로 나누는 행렬의 형태이다
  • 상삼각행렬(Upper Triangular Matrix)은 주대각선 아래의 성분이 모두 0인 정사각행렬이다.
  • 하삼각행렬(Lower Triangular Matrix)은 주대각선 위의 성분이 모두 0인 정사각행렬이다.
• Ax + b의 형태에서 LUx = b 형태로 변환할 수 있고 Ux = y 로 대입해 Ly = b 라는 식을 이끌어 낼 수 있다
• LU분해를 쓰는 이유는 아래와 같이 있다 
  • 수치적 안정성
  • b가 자주업데이트 되는 경우 연산 속도의 향상

5. 행렬의 다양한 용어

• 스칼라 : 어느 한 원소만을 가지고 있는것 (점과 유사)
• 벡터 : 스칼라의 집합으로 만들어진 1 x N 혹은 N x 1의 행렬(선과 유사)
• 행렬 : 직사각형 구조에 숫자들을 담아 놓은 구조 -> 열벡터나 행벡터들의 모음
• 전치행렬: NxM의 행렬을 MxN의 행렬로 바꿔 놓은 형태
• 영행렬 : 모든 원소의 값이 0인 행렬
• 정방행렬: NxN의 정사각형 행렬
  • 주대각선: 정방 행렬에서 a(i,i)들의 집합
  • 항등행렬: 주대각선은 모두 1이고 나머지는 0인 정방행렬
• 행렬의 합과 곱:
  • 행렬의 합: A,B행렬의 모든 행과 열의 갯수가 갓을때 C(i,j) = A(i,j)+B(i,j)로 표현
  • 행렬의 곱:m*r의 A행렬과 r*n의 행렬에 대해 AB = C에서 C(i,j) = A(i,1)*B(1,j)+A(i,2)*B(2,j)....A(i,r)*B(r,j)로 정의
    • 행렬의 곱에서 일반적으로 A*B ≠  B*A 이고 A*(B*C) ≠ (A*B)*C이다
• 텐서: 스칼라, 벡터, 행렬을 아우르는 개념, 숫자가 늘어설 수 잇는 방향이 K면 K-텐서로 부름
  
  • 스칼라 -> 0-텐서, 벡터 -> 1-텐서, 행렬 -> 2-텐서
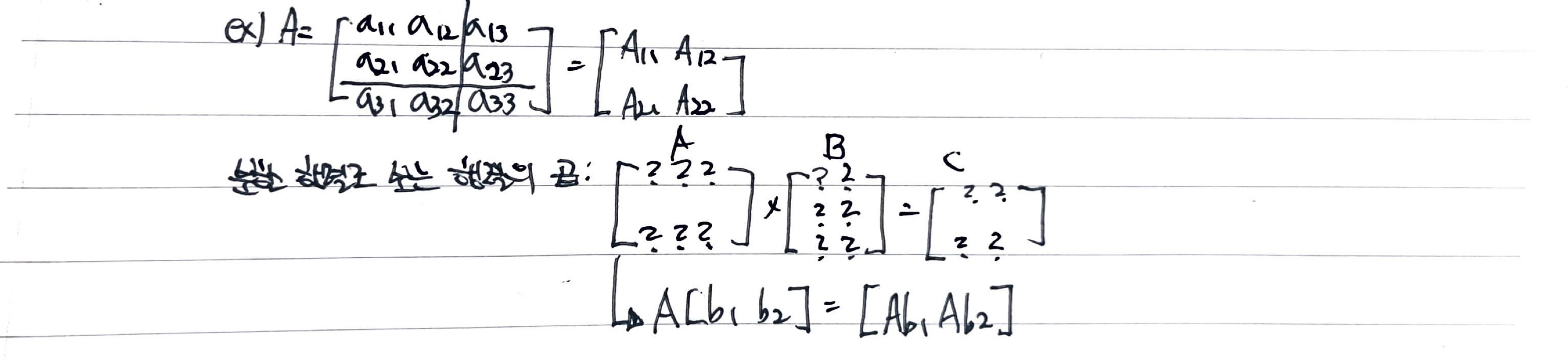
• 분할 행렬: 행렬을 몇개의 조각 단위로 분할하여 생각한 것

6. 선형 조합

• 행렬은 열벡터의 리스트들이다
• Ax는 행렬 A가 가지고 있는 열벡터의 선형 조합이다
  •  x1a1 + x2a2...+xnan
• 선형대수에서 이처럼 벡터들에 대한 가중치의 합이 선형 조합이라고 한다
• 행렬 A의 열벡터들의 대한 모든 선형 조합의 결과를 모아 집합으로 구성될 때 그 집합을 열공간이라고 하며 col(A)로 표현된다

7. 좌표계 변환

• 좌표계를 도입한 후 시작점을 원접으로 맞추고 끝점을 v로 표현한것
• 좌표계 변환: 아래와 같이 변환 벡터들의 곱을 해당 축과의 좌표로 변환 할 수 있다

8. 선형 변환

• 선형 함수: 임의의 함수 f가 두가지 조건을 만족하면 f를 선형 함수라고 한다
  • f(x+y) = f(x) + f(y)
  • f(cx) = c*f(x)
•  함수의 입력이 n-벡터이고 출력이 m벡터인 함수 T를 변환이라고 한다.
  • T:Rn⟶Rm
• 특별히 n = m이면 연산자(operation)이라고 한다
• 여기서 선형 함수의 성질을 만족하면 선형 변환이라고 한다

• 선형 변환에 대한 코딩
  1. 구현하고자 하는 function과의 입력과 출력이 벡터로 정의 되는지 확인
  2. 구현하고자 하는 기능이 선형인지 확인
  3. 입력이 n-벡터고 출력이 m벡터면 m*n표준 행렬 구성
• 표준행렬을 이용한 선형변환 코딩
  • 다음의 m×n 표준행렬(standard matrix)을 구성함으로써, 우리가 원하는 방식대로 동작하는 행렬변환 TA​:Rn⟶Rm을 코딩할 수 있다
    • A=[TA​(e1​)TA​(e2​)⋯TA​(en​)]m×n​